Dalam kehidupan sehari-hari selalu menggunakan perhitungan. Terkadang semua orang cepat melupakan, dengan berbagai macam alasan, sudah tua, tidak ingat lagi, pelajaran itu sudah tak diingat lagi ataupun terkadang lucu jawabannnya "terlalu banyak yang dipikirkan, bukan mau ingat rumus itu aja", sangat miris. Rumus matematika bukan hapalan tetapi memerlukan pemahaman, mudah mudahan bisa diingat terus.
Penulis mencoba kembali mengingatkan rumus rumus matematika, siapa tahu dapat membantu. Di Artikel ini penulis mencoba memaparkan asal rumus tersebut.
Rumus Bangun Datar :
Bangun datar yang merupakan sebutan untuk bangun-bangun dua dimensi memiliki sifat masing-masing yang berbeda satu sama lain. Berikut ini penjelasan mengenai sifat-sifat bangun datar.
Rusuk terpanjang disebut sebagai panjang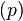 dan rusuk terpendek disebut sebagai lebar
dan rusuk terpendek disebut sebagai lebar 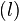 .
.
Bangun datar yang merupakan sebutan untuk bangun-bangun dua dimensi memiliki sifat masing-masing yang berbeda satu sama lain. Berikut ini penjelasan mengenai sifat-sifat bangun datar.
- Persegi Panjang
Rusuk terpanjang disebut sebagai panjang
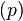 dan rusuk terpendek disebut sebagai lebar
dan rusuk terpendek disebut sebagai lebar 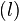 .
.
Berikut ini cara mencari komponennya, keliling (K), Luas (L) dan Diagonal (d)
 |
| Komponen Persegi Panjang |
- Persegi / Bujur Sangkar
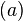 yang sama panjang dan memiliki empat buah sudut yang kesemuanya adalah sudut siku-siku. Bangun ini dahulu disebut sebagai bujur sangkar.
yang sama panjang dan memiliki empat buah sudut yang kesemuanya adalah sudut siku-siku. Bangun ini dahulu disebut sebagai bujur sangkar.
Berikut ini cara mencari komponennya ;
- Segitiga
Segitiga atau segi tiga adalah nama suatu bentuk yang dibuat dari tiga sisi yang berupa garis lurus dan tiga sudut. Matematikawan Euclid yang hidup sekitar tahun 300 SM
menemukan bahwa jumlah ketiga sudut di suatu segi tiga pada bidang
datar adalah 180 derajat. Hal ini memungkinkan kita menghitung besarnya
salah satu sudut bila dua sudut lainnya sudah diketahui.
Menurut panjang sisinya:
Segitiga sama sisi adalah segitiga yang ketiga sisinya sama panjang. Sebagai akibatnya semua sudutnya juga sama besar, yaitu 60o.
Segitiga sama kaki adalah segitiga yang dua dari tiga sisinya sama panjang. Segitiga ini memiliki dua sudut yang sama besar.
Segitiga sembarang adalah segitiga yang ketiga sisinya berbeda panjangnya. Besar semua sudutnya juga berbeda.
 |
 |
 |
| Segitiga sama sisi | Segitiga sama kaki | Segitiga sembarang |
Menurut besar sudut terbesarnya:
Segitiga siku-siku adalah segitiga yang salah satu besar sudutnya sama dengan 90o. Sisi di depan sudut 90o disebut hipotenusa atau sisi miring.
Segitiga lancip adalah segitiga yang besar semua sudut < 90o
Segitiga tumpul adalah segitiga yang besar salah satu sudutnya > 90o
 |
 |
 |
| Segitiga siku-siku | Segitiga tumpul | Segitiga lancip |
Berikut ini cara mencari komponennya ;
 |
| Komponen Segitiga |
- Jajaran genjang
Jajar genjang atau Jajaran genjang (inggris parallelogram) adalah bangun datar dua dimensi yang dibentuk oleh dua pasang rusuk yang masing-masing sama panjang dan sejajar dengan pasangannya, dan memiliki dua pasang sudut yang masing-masing sama besar dengan sudut di hadapannya.
Berikut ini cara mencari komponennya ;
 |
| Komponen Jajaran Genjang |
- Belah Ketupat
Belah ketupat (inggris rhombus) adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang sama panjang, dan memiliki dua pasang sudut bukan siku-siku yang masing-masing sama besar dengan sudut di hadapannya.
Belah ketupat merupakan jajaran genjang yang rusuknya sama panjang.
Belah ketupat dapat dibangun dari dua buah segitiga sama kaki identik yang simetri pada alas-alasnya.
Berikut ini cara mencari komponennya ;
 |
| Komponen Belah Ketupat |
- Layang-layang
Berikut ini cara mencari komponennya ;
 |
| Komponen Layang - Layang |
- Trapesium
Berikut ini cara mencari komponennya ;
 |
| Komponen Trapesium |
- Lingkaran
Elemen-elemen yang terdapat pada lingkaran, yaitu :
 |
| Elemen Lingkaran |
- Elemen lingkaran yang berupa titik, yaitu :
- Titik pusat (P)
merupakan titik tengah lingkaran, dimana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.
- Titik pusat (P)
- Elemen lingkaran yang berupa garisan, yaitu :
- Jari-jari (R)
merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran. - Tali busur (TB)
merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda. - Busur (B)
merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran. - Keliling lingkaran (K)
merupakan busur terpanjang pada lingkaran. - Diameter (D)
merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas. - Apotema
merupakan garis terpendek antara tali busur dan pusat lingkaran.
- Jari-jari (R)
- Elemen lingkaran yang berupa luasan, yaitu :
- Juring (J)
merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya. - Tembereng (T)
merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya. - Cakram (C)
merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.
- Juring (J)
Berikut ini cara mencari komponennya ;
 |
| Komponen Segitiga |
 |
| Elemen Segitiga |
Rumus Bangun ruang akan saya bahas di sini
Update 30 Jan 2015
23 Feb 2015
Sumber : Wikipedia, Toms Pro Arsip
Postingan ini belum sempurna, karena keterbatasan waktu. Penyusun akan selalu menambahkan dilain hari
Artikel Terkait












0 komentar:
Posting Komentar